Welcome and Happy New Year. I made a small tweak to the model, rearranging the layout of some of the initial settings, and to derive inertia from installed synchronous capacity rather than synchronous supply. An updated copy of the spreadsheet is available here (version 1.2).
Please remember, the model’s purpose is to help understand the transient response of power network. It’s not an exact model for a number of reasons – and some of the reasons I’ll expand on as I describe the variables and equations.
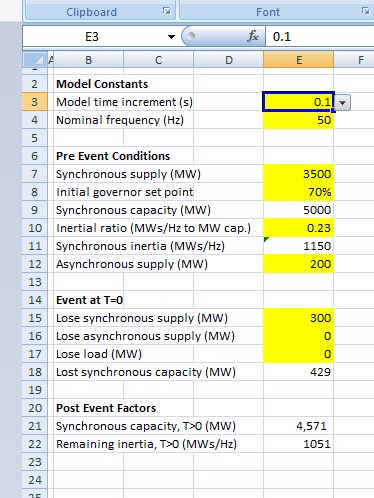
Here is the portion of the worksheet we are looking at with this post.
Model Constants
Model time increment [E3]: The time interval over which we calculate each step. I have set this to 0.1 second. Using the cell drop down you can also select either 0.05 or 0.2 second. Changing the step size affects model resolution and the overall time duration modelled.
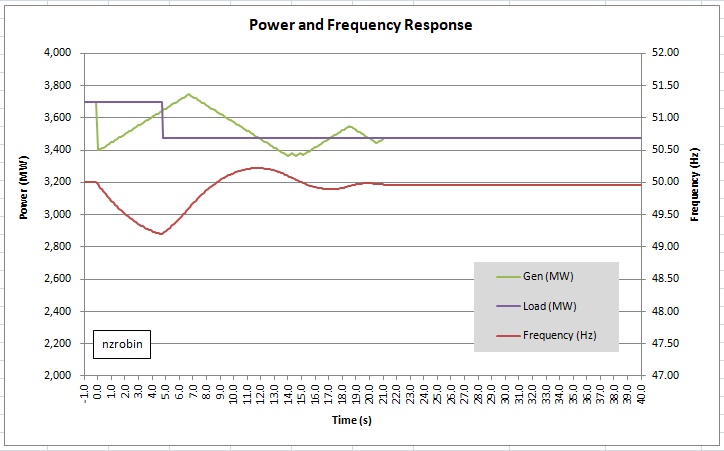
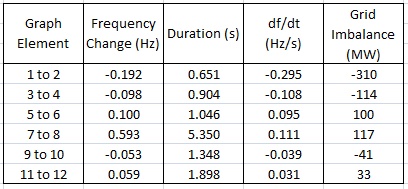
Nominal Frequency [E4]: System nominal frequency. It is adjustable but I recommend leaving it at 50 Hz. I have fixed the scales of the primary and secondary axes of the graph to make use of common horizontal lines. Further, the 47 Hz minimum and 52 Hz maximum align with the frequencies where cascade tripping (blackout) is likely to occur. The red line (frequency) has to stay within the window.
Pre Event Conditions
Synchronous supply (MW) [E7]: This the combined output of all of the synchronous generators on the network. It isn’t their capacity or rating; it is their MW output just before the disturbing event.
The net power being injected into the network is the sum total of the Synchronous supply (MW) [E7] and Asynchronous supply (MW) [E12]. As mentioned above I have fixed the scales on the graph. The power scale is set to 2000 MW to 4000 MW, so to see what is going on, keep the total output toward the middle of that range. The network is presumed balanced (stable) pre-event, therefore net generation equals net connected load (plus grid losses).
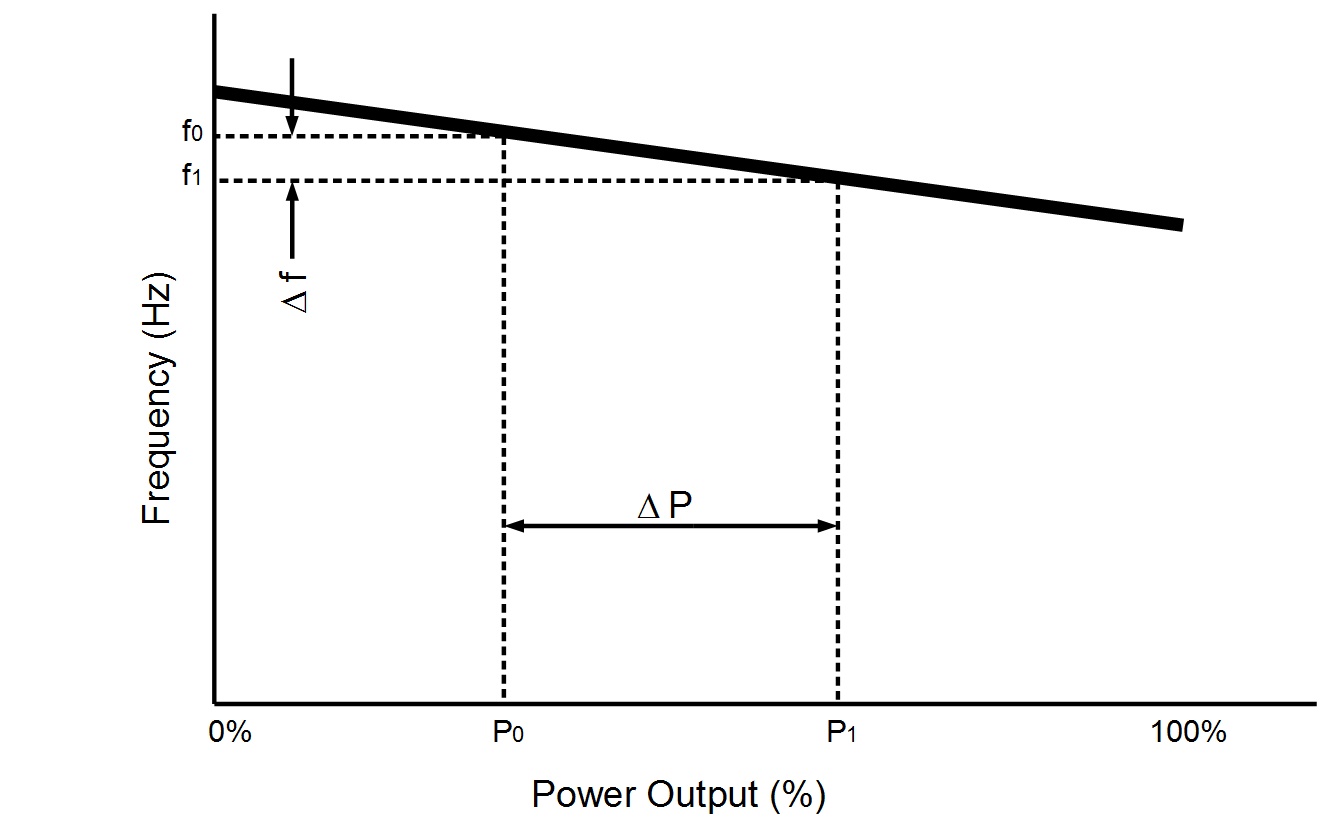
Initial governor set point (%) [E8]: This setting defines the pre-event ‘average’ operating point of the synchronous machines.
Why ‘average’? A simplification made is that the synchronous machines on the grid are rolled up into one large machine with a single set of control characteristics. The real system (of course) has many machines operating, each with its own governor. Whilst the governors should have similar droop characteristics, they will be at various set points, and each should take account of the different response capability expected of its controlled machine. The Initial governor set point in the model represents an ‘average’ of all the operating synchronous machines on the grid. It is related to the spinning reserve. The MW difference between the set point in terms of MW, and the total of the synchronous machine capacities’, is ‘spinning reserve’.
Synchronous capacity (MW) [E9]: This is the pre-event net total of the output power ratings of all the synchronously connected generators. It is derived from the above two factors: E9=E7/E8.
Inertial ratio (MWs/Hz to MW capacity) [E10]: This is the available rotational kinetic energy in megawatt seconds, per Hertz of speed change, per megawatt of synchronous machine rating.
Another simplification made is the relationship between kinetic energy and speed. Kinetic energy of a rotating mass is proportional to the square of rotational speed, and therefore dependent on frequency. However as we’re interested in speed (frequency) changes near to 50 Hz, (within 2 or 3 Hz) we don’t lose much accuracy by taking the kinetic energy as proportional to frequency (i.e.: linear for that small range / a constant inertial ratio).
Synchronous inertia (MWs/Hz) [E11]: This is the pre-event net total inertia. It is derived from the above two factors: E11=E9*E10.
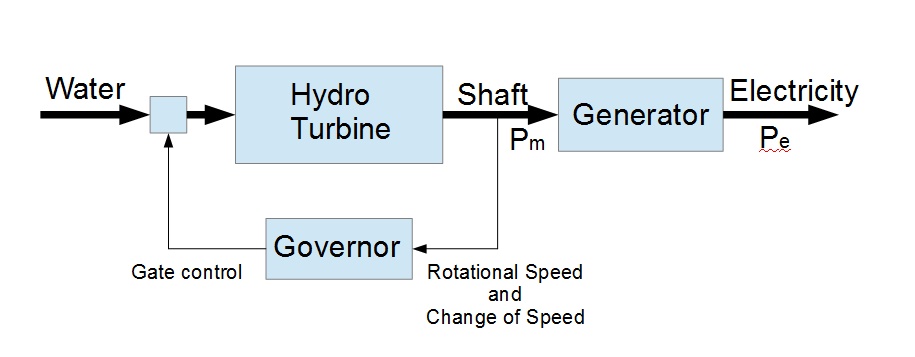
Asynchronous supply (MW) [E12]: This is the combined megawatt output from all of the asynchronous generators on the network. This would generally be the combined output of all the wind and solar generation at the time of the event.
It may not be, but given the short duration modelled, this generation is taken as constant through the event period (unless we have chosen it as the loss event, or unless we have chosen to turn on IBFFR, Inertia Base Fast Frequency Response. There’ll be more on IBFFR in a later post).
Event at T=0
Three types of event are allowed. Choose the event by entering the MW disturbance in the appropriate cell.
Lose synchronous supply (MW) [E15]: Entering a number of MW in this cell represents loss of synchronous generation, at its pre event operating level. (i.e.: not the MW generator capacity). Losing synchronously generated MW affects both remaining inertia and available generation.
Lose asynchronous supply (MW) [E16]: Entering a number of MW in this cell represents loss of asynchronous generation, at its pre event operating level. (i.e.: not the generator MW capacity). Whilst losing asynchronous generation does reduce available generation, it does not reduce remaining inertia (because it offered none in the first place).
Lose load (MW) [E17]: The third type of event that can be simulated is a loss of load, i.e.: maybe the loss of a major feed into a city or a region. This should be a rare type of event (often referred to as non-credible) given that the network at this level should have built-in redundancy and it would take a double failure for it to occur. A loss of load event results in a frequency rise rather than a decline, generation input exceeds demand and the generators speed up.
Lost synchronous capacity (MW) [E18]: With the loss of synchronous supply also comes loss of synchronous capacity, and this is estimated in this model to be in proportion to the lost supply and inverse of the initial governor set point. It is derived from these two factors where E18=E15/E8.
Post Event Factors
Synchronous capacity, T>0 (MW) [E21]: This field calculates the remaining synchronous capacity after the disturbing event by deducting the lost synchronous capacity from that prior to the event, i.e.: E21=E9-E18.
Remaining inertia, T>0 (MWs/Hz) [E22]: This field calculates the remaining synchronous inertia after the disturbing event from the remaining synchronous capacity and inertial ratio, i.e.: E22=E21*E10.
That’s enough for now. The next post will focus on governor characteristics.